Un graphe sera dit connexe si, pour tout couple de sommets, il existe une chaîne allant de l'un à l'autre.
Connexe signifie concrètement : "d'un seul tenant" Ce graphe n'esrt pas connexe car le sommet d est isolé
Si un graphe n'est pas connexe, on appellera composante connexe, chacun de ses "morceaux" connexes.
Plus formellement :
On définit une relation entre les sommets de la manière suivante : xRy si et seulement si x=y ou x et y sont reliés par une chaîne. On démontre aisément que cette relation R est réflexive, symétrique et transitive, donc que c'est une relation d'équivalence. Qui dit "relation d'équivalence", dit "classes d'équivalence". On appellera ces classes des composantes connexes.
On notera en général : p, le nombre de composantes connexes d'un graphe.
On peut s'intéresser au nombre de sommets à supprimer pour "disconnecter" un graphe connexe (i.e. faire qu'il ne soit plus connexe).
Remarque : Quand on enlève un sommet, on supprime aussi tous les arcs dont ce sommet est extrémité.
Le nombre minimum de sommets pour ce faire sera noté κ, on l'appellera la connectivité du graphe.
Un graphe sera dit h-connexe si sa connectivité est supérieure ou égale à h (donc, si on ne peut le disconnecter en enlevant h-1 sommets).
On qualifiera d'ensemble d'articulation, un ensemble de sommets dont la suppression disconnecte le graphe. La connectivité est donc le cardinal minimal d'un ensemble d'articulation.
ATTENTION
cela ne veut pas dire que ce sera le cas avec k sommets quelconques
|
|
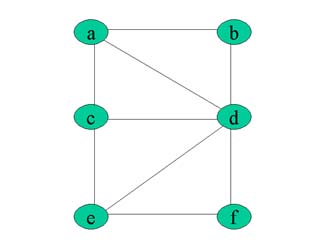 |
Ce graphe est connexe.
Quelque soit le sommet qu'on retire, il reste connexe.
Si on retire b et d, le graphe est toujours connexe.
Si on retire c et d le graphe n'est plus connexe.
Le Graphe est donc 2-connexe.
{c,d} est un ensemble d'articulation du graphe
|
Remarque : Si un graphe est 3-connexe, il est 2-connexe.
Un point d'articulation est un sommet dont la suppression disconnecte le graphe.
Un isthme est un arc qui a le même effet.
|
|
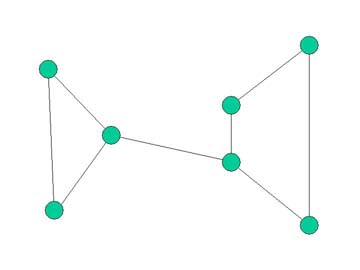 |
Ce graphe est connexe.
Il possède deux points d'articulation.
L'arc central est un isthme.
Il n'y a aucun autre isthme.
|