Un graphe est composé d'un ensemble de sommets et d'un ensemble d'arcs; on note X l'ensemble des sommets
Un arc est un couple de sommets, donc, un élément du produit cartésien XxX; on note U la famille des arcs.
Ainsi le graphe (noté, par exemple : G) sera-t-il égal au couple (X,U)
Le nombre de sommets est appelé l'ordre du graphe et sera, en général, noté : n
En général, les sommets d'un graphe seront représentés par des points de l'espace et les arcs par des flèches allant d'un point à un autre, c'est ce qu'on appelle la représentation sagittale du graphe :
Dans un arc (x,y) : x est l'extrémité initiale et y l'extrémité finale.
Un arc de la forme (x,x) est une boucle.
On dit que y est un successeur de x s'il existe un arc (x,y); on dit aussi que x est un prédécesseur de y. |
|
Dans cet exemple, on a la représentation sagittale d'un graphe d'ordre 6.
X = {a,b,c,d,e,f}
U = {1,2,3,4,5,6,7,8}
L'arc 7 est une boucle |
|
On n'étudiera que les graphes simples : un graphe sera dit simple s'il n'y a pas plusieurs arcs ayant la même extrémité initiale et la même extrémité finale et s'i ln'y a pas de boucle. Le graphe de l'exemple précédent n'est pas simple : pour le rendre simple, il faut supprimer la boucle (a,a) et l'arc 8.
Un graphe simple est un graphe sans boucle tel qu'entre deux sommets différents, il y ait au plus un arc. Dans un graphe simple, on pourra donc noter un arc à l'aide de ses extrémités initiale et finale. Dans un graphe simple, on peut parler de l'ensemble des arcs. Deux arcs sont dits adjacents s'ils ont une extrémité en commun. Deux sommets sont dits adjacents si un arc les relie.
Le demi-degré extérieur d'un sommet x (noté dG+(x)) est égal au nombre d'arcs qui "partent" de x. Le demi-degré intérieur d'un sommet x (noté dG-(x)) est égal au nombre d'arcs qui "arrivent" en x. Le degré du sommet x (noté dG(x)) est égal à la somme des demi-degrés.
|
|
Vous noterez que rien n'interdit la présence dans le graphe de l'arc (e,f) et (f,e). d est un sommet isolé : il n'est relié à aucun autre a et b sont adjacents l'arc 4 est incident à f b et e sont des prédécesseurs de f b et e sont des successeurs de a le demi-degré extérieur de e = 1 le demi-degré intérieur de e = 2 le degré de e = 3
|
|
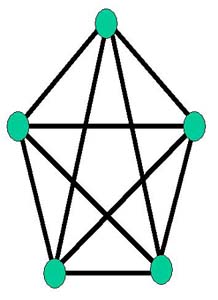 K5 K5 |
Un graphe est dit complet si deux sommets différents quelconques sont reliés. On parle aussi de clique pour un graphe complet.
Quand un graphe n'est pas complet, don ensemble de sommets peut être partitionné en cliques : On notera ω le nombre maximal de sommets d'une clique sous-graphe. On notera θ le nombre minimal de cliques nécessaires pour partitionner l'ensemble des sommets du graphe.
|
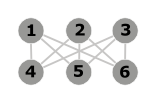 K3,3 K3,3
|
Un graphe est dit biparti si l'ensemble de sommets peut être partitionné en deux classes de sorte que les sommets d'une même classe ne soient jamais adjacents. Les graphes de fonctions, applications, bijections sont des graphes bipartis On définit aussi des graphes bipartis complets, notés Km,n
|
On appelle sous-graphe engendré par A (partie de X) le graphe obtenu en ne
conservant que les sommets de A et les arcs les reliant.
On peut définir un sous-graphe partiel.
Par exemple, si on considère le graphe des routes de France, on parlerait du graphe partiel des Routes Nationales, du sous-graphe des Routes de normandie et du sous-graphe partiel des Routes Nationales de Normandie.
|
|
On appelle chaîne une succession d'arcs, chaque arc intermédiaire de la séquence ayant une extrémité en commun avec l'arc précédent et l'autre extrémité en commun avec l'arc suivant.
Une chaîne ne rencontrant pas deux fois le même sommet est dite élémentaire. Une chaîne ne rencontrant pas deux fois le même arc est dite simple.
On appelle chemin une chaîne "bien orientée", c'es t à dire que tous les arcs de la chaîne sont parcourus dans le bon sens.
Ce n'est pas nécessairement le cas dans une chaîne, où on peut rencontrer des arcs directs (parcourus dans le bon sens) et des arcs inverses.
On appelle cycle une chaîne simple qui "boucle" : les arcs de début et de fin sont adjacents par leur sommet libre.
On appelle circuit un cycle "bien orienté", à la fois cycle et chemin. |
|
(1,4,5) est une chaîne dont les arcs 1 et 4 sont directs et 5 inverse
(7,2,1,4) est un chemin : tous les arcs sont parcourus dans le bon sens.
(1,4,5,2) est un cycle , les extrémités "libres" des arcs 1 et 2 sont égales; (a,b) puis (b;f) puis (e,f) puis (e,a)
(6,7,2) est un circuit
|
|
On appelle chaîne eulérienne une chaîne empruntant tous les arcs du graphe une fois et une seule.
On appelle chaîne hamiltonnienne une chaîne passant par tous les sommets du graphes une fois et une seule.
On peut bien évidemment étendre les deux notions précédentes aux chemins, cycles, circuits.
Les notions d'eulérien et d'hamiltonien sont des notions duales (dualité sommets-arcs) . |
|
|
Télécharger le Diaporama en PDF
|
|