 |
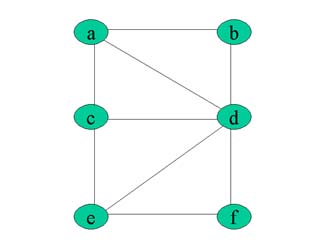
La distance entre deux sommets d'un graphe connexe (ou entre 2 sommets d'une même composante connexe d'un graphe non connexe) est le nombre minimum d'arcs (on dit aussi la longueur) d'une chaîne allant de l'un à l'autre. Dans l'exemple ci-contre la distance de a à f est de 2 : on peut aller de a à f en 2 arcs, mais pas en 1 arc.
L'écartement d'un sommet est la distance maximale existant entre ce som met et les autres sommets du graphe. (si le graphe n'est pas connexe, l'écartement est infini). Dans l'exemple ci-contre, l'écartement de a est de 2, comme d'ailleurs pour tous les autres sommets, sauf d dont l'écartement vaut 1.
On appelle centre d'un graphe, le sommet
d'écartement minimal. Par exemple, dans une clique, tous les sommets sont "centres"
On appelle rayon d'un graphe G, noté ρ(G), l'écartement d'un centre de G. Le rayon est de 1 dans l'exemple. d est le seul centre de ce graphe.
On appelle diamètre d'un graphe
G, noté δ(G),
la distance maximale entre deux sommets du graphe G.
|